poj1286–Necklace of Beads

标签：数学 置换 polya定理

---

题目描述

给出三种颜色红绿蓝，对一串n（n<24）个小球的环染色，环可以旋转和翻转，问最终可能有多少不同的染色方案。

输入输出格式

Input
The input has several lines, and each line contains the input data n.
-1 denotes the end of the input file.

Output
The output should contain the output data: Number of different forms, in each line correspondent to the input data.

输入输出样例

Sample Input
4
5
-1
Sample Output
21
39

题解

首先给出两个定理:
Burnside引理:
$$\frac{1}{\left | G \right |}\sum_{i=1}^{n}D(a_{i})$$
其中G表示置换种类（需要记住的是不变置换也算一种置换）
$D(a_{i})$表示在i置换下不动点的个数
Polya定理:
$$\frac{1}{\left | G \right |}\sum_{i=1}^{n}m^{c(g_{i})}$$
其中m表示染色种类，$c(g_{i})$表示在第i种置换下的循环节个数
这里有一个讲得比较好的文库可惜我没有下载券不能下载…
那么对于这道题来说要分两种情况:
1.旋转
对于旋转一共有0~n-1共n种置换,对于旋转i,它的循环节为gcd（n,i）,这个可以找找规律发现，也可以通过证明:
假设每次增量为p,最少走了k步又回到原点:
则kp % n = 0 而 kp % p = 0且k为最少,故kp是n,p的最小公倍数，kp = lcm（n,p）
那么每次走了kp / p = lcm（n, p） / p = k步
那么一共走了n / （lcm（n,p）/ p） = np / lcm（n,p）= gcd（n,p）次
所以循环节是gcd（n,p）。
所以$Ans = Ans + \sum_{i=0}^{n-1}3^{gcd(n,i)}$
2.翻转
这里要分奇偶讨论:
（1）偶数
这里存在两种对称方式，如图: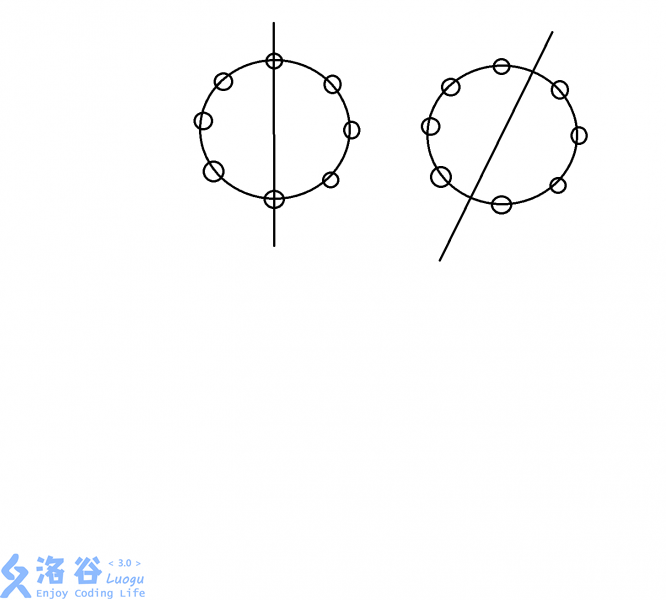

一种是一条对称轴穿过两个点，此时有n/2种置换，对于每种置换有n/2 + 1个循环节
另一种是一条对称轴穿过两点之间，此时有n/2种置换，对于每种置换有n/2个循环节
（2）奇数
这里就只有一种对称方式了,选每个点作为对称点共有n中置换,对于每个置换有n/2 + 1个循环节
最后Ans除以G（2n中置换）即可

代码

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#define ll long long
using namespace std;

int n;

int gcd(int a, int b) {return !b ? a : gcd(b, a % b);}

ll pow_mul(int a, int b)
{
    ll ans = 1;
    while(b)
    {
        if(b % 2) ans = ans * a;
        a = a * a;
        b >>= 1;
    }
    return ans;
}

int main()
{
    while(scanf("%d", &n) && n >= 0)
    {
        ll ans = 0;
        if(n == 0) {printf("0\n"); continue;}
        for(int i = 0; i < n; i ++) 
            ans += pow_mul(3, gcd(n, i));
        if(n % 2)
        {
            ans += pow_mul(3, n / 2 + 1) * n;
        }    
        else
        {
            ans += pow_mul(3, n / 2) * (n / 2);
            ans += pow_mul(3, n / 2 + 1) * (n / 2);
        }
        printf("%lld\n", ans / (2 * n));
    }
    return 0;
} 

心得

运用polya定理主要是找出循环节，但是值得注意的是，polya定理不能受到颜色数量的限制，否则只能用Burnside引理，而且注意要包括不变置换。