SHOI2006 有色图
标签: 数学 置换 polya定理
题目描述
如果一张无向完全图(完全图就是任意两个不同的顶点之间有且仅有一条边相连)的每条边都被染成了一种颜色,我们就称这种图为有色图。如果两张有色图有相同数量的顶点,而且经过某种顶点编号的重排,能够使得两张图对应的边的颜色是一样的,我们就称这两张有色图是同构的。以下两张图就是同构的,因为假如你把第一张图的顶点(1,2,3,4)置换成第二张图的(4,3,2,1),就会发现它们是一样的。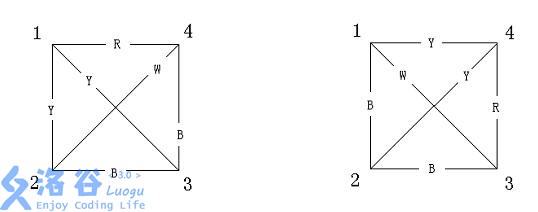
你的任务是,对于计算所有顶点数为n,颜色种类不超过m的图,最多有几张是两两不同构的图。由于最后的答案会很大,你只要输出结论模p的余数就可以了(p是一个质数)
输入输出格式
输入格式:
输入文件只有一行,由三个正整数n,m,p组成,他们满足1≤n≤53,1≤m≤1000,n<p≤10^9
输出格式:
即总数模p后的余数
输入输出样例
输入样例#1:
1 1 2
输出样例#1:
1
输入样例#2:
3 2 97
输出样例#2:
4
输入样例#3:
3 4 97
输出样例#3:
20
题解
06年就出来了这种题吗…ORZ
那么这道题难点在于是点置换,边染色,因此我们必须通过点置换找出边置换的循环节。
首先,我们可以把边分为两类:
1.边的两个端点处于同一循环节中
2.边的两个端点处于不同循环节中
那么下面就对这两种情况进行讨论
(1)在同一循环节内:
我们假设循环节的长度为$l$,可以想象成这$l$个点分别分布在等$l$边形的定点上
1.若$l$为奇数
则随着点的置换,每条边相当于顺时针移动到下一条边,故边的每个循环节长度都为$l$,而总边数为$\frac{l(l-1)}{2}$,所以循环节个数为$\frac{l-1}{2}$
2.若$l$为偶数
同样用上述方式思考,不过会存在跨越180°的情况,那么这些边存在多少呢,画一画图就可以发现存在$\frac{l}{2}$条,所以此时循环节个数为$$\frac{\frac{l(l-1)}{2} - \frac{l}{2}}{l}+1=\frac{l}{2}$$
(1)在不同循环节内
假设两个循环节长度分别为$l1$和$l2$
假设一条边最少经过$k$次变换回到本身(这里的变换也可以理解为两个端点的在某种置换规则下的同时变换)
那么k % l1 = 0 且 k % l2 = 0
所以k = lcm(l1, l2),而一共有多少条边呢,肯定是l1 * l2条嘛(乘法原理撒)
所以循环节个数为
$\frac{l1*l2}{lcm(l1,l2)}=gcd(l1,l2)$
那么综上所述,我们已知某次点置换的循环节长度和个数之后,我们就可以得到边置换的循环节长度:
$$g=\sum_{i=1}^{n}\left \lfloor \frac{l_{i}}{2} \right \rfloor+\sum_{i=1}^{n}\sum_{j=i+1}^{n}gcd(l_{i},l_{j})$$
OK…总算是找到点置换与边置换的关系了,只要我们找到关于点置换的循环节,对应的我们就可以求出边置换的循环节了。
对于此题n<=53我们直接暴力的话复杂度是$O(53!)$是妥妥爆炸的,但是我们发现,我们只需要知道置换的循环节的长度和数量即可,对于里面的元素是什么我们不关心的,因此我们可以考虑对n进行整数拆分,即枚举点置换的循环节长度:
$l1<=l2<=l3<=….<=ln$
相当于我们把$n$个点分别放进大小为$l1,l2,…,ln$的循环节中,相当于一个多重全排列:$$\frac{n!}{\prod_{i=1}^{n}li!}$$
然后对于每一个循环节内部元素顺序分配,相当于一个圆排列:$(li-1)!$
算到这里,我们发现循环节本身是没有顺序之分的,即:
$(1,2,3)(4,5,6)$等价于$(4,5,6)(1,2,3)$但是上述计算会导致循环节长度相同的$li$会因为顺序原因导致算重(这里不用考虑循环节长度不同,因为我们是按照从小到大枚举的嘛)因此设长度相同的循环节有$c$个,则答案最终要除以$c!$
综上所述,方案数为:
$$Sum = \frac{\frac{n!}{\prod_{i=1}^{n}li!}*(li-1)!}{\prod_{i=1}^{n}ci!}$$
$$Sum = \frac{n!}{\prod_{i=1}^{n}li*ci!}$$
因此:
$$Ans = \frac{Sum*m^{g}}{\left | G \right |}$$
(细心的童鞋可以发现$Sum$中$n!$可以和$G$抵消哟~)
代码
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#define ll long long
#define N 70
#define debug system("pause")
using namespace std;
ll n, m, p;
ll num[N], d[N];
ll fac[N], ans = 0;
ll gcd(int a, int b) {return !b ? a : gcd(b, a % b);}
ll pow_mul(ll a, ll b)
{
ll ans = 1;
while(b)
{
if(b & 1) ans = ans * a % p;
a = a * a % p;
b >>= 1;
}
return ans;
}
void calc(int cnt)
{
memset(num, 0, sizeof(num));
ll mul = 1; ll c = 0;
for(int i = 1; i <= cnt; i ++)
{
num[d[i]] ++;
mul = mul * d[i] % p;
c += d[i] / 2;
for(int j = 1; j < i; j ++)
c += gcd(d[i], d[j]);
}
for(int i = 1; i <= n; i ++)
mul = mul * fac[num[i]] % p;
//for(int i = 1; i <= cnt; i ++) printf("%d ", d[i]);
//printf("%lld %lld\n", c, mul); debug;
ans = ans + (pow_mul(mul, p - 2) * pow_mul(m, c) % p);
ans %= p;
//printf("%lld %lld %lld", ans, t1, t2); debug;
}
void dfs(int tot, int cnt, int pre)
{
d[cnt] = tot;
calc(cnt);
for(int i = pre; i <= tot - i; i ++)
{
d[cnt] = i;
dfs(tot - i, cnt + 1, i);
}
}
int main()
{
scanf("%lld%lld%lld", &n, &m, &p);
fac[0] = fac[1] = 1;
for(int i = 2; i <= n; i ++) fac[i] = fac[i - 1] * i % (ll)p;
dfs(n, 1, 1);
printf("%lld", ans);
return 0;
}
/*
53 1000 131071
*/
心得
听大佬们说这是一种套路题,掌握方法就可以了。其实想一想这类题相当于是已知一种元素的置换方式,并且这种元素的二元组决定另一种元素,求另一种元素的本质不同方案数(两个点确定一条边嘛,所以由点的二元组决定一条边)那么是否由此可以推广到多元组呢…?(不过会讨论情况讨论到疯掉吧…)

![[HNOI2008]Cards](http://pvujsoqjl.bkt.clouddn.com/MN2deerstalker.png)